Example
Let’s go through an example. We’ll construct a model in which an
- intracellular cell cycle network (ODE) regulates
- the division of motile cells which (CPM)
- release a diffusive cytokine (PDE) which, in turn,
- controls the cell cycle (ODE).
Thus, there are 3 sub-models (ODE, CPM and PDE) that interact in a cyclic fashion:
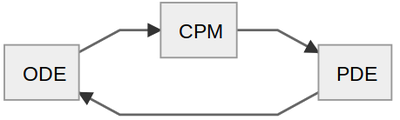
Step 1: Intracellular Model (ODE)
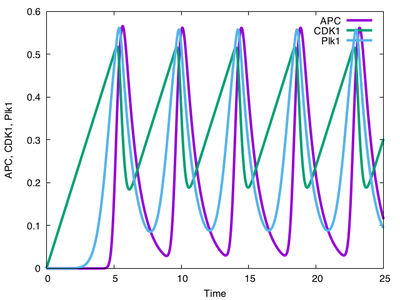
First, we define a ODE model of a cell cycle that we take directly from Ferrell et al. 2011.
Check out CellCycle.xml to try yourself via:
- Morpheus Link or
- Morpheus GUI:
Examples→ODE→CellCycle.xmlor - Morpheus Model Repository.
In Morpheus, we can describe the same system of equations together with the parameter values as below:

CellType scope.
The System is defined within a CellType. This makes sure that the ODE system is calculated separately for each member of the population of this cell type. Furthermore the variables are defined as Properties. These are variables that are bound to a particular cell such that each cell can have a different value for this variable.
If you run this model for a single cell with the parameters above, you will see oscillatory behavior:
Step 2: Cell-Based Model (CPM)
Now, we would like to couple the above model to control the ‘physical’ cell division of a spatial cell model. This can be achieved easily by adding a few elements.
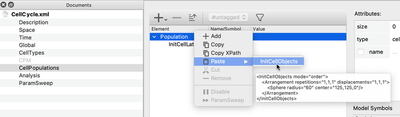
First, we change the space to be a square Lattice, sized 250x250. We initialize our cell centrally using the Populations' InitCellObjects component. We also use Gnuplotter in the Analysis section to check the results.
<InitCellObjects mode="order">
<Arrangement displacements="1, 1, 1" repetitions="1, 1, 1">
<Sphere center="125, 125, 0" radius="60"/>
</Arrangement>
</InitCellObjects>
Instead of adding one element after the other with the + button or right click/Add in the GUI, you can select the above XML snippet and drag and drop it onto the Population or paste it via the context menu.
Second, we add a VolumeConstraint and SurfaceConstraint that control the area and shape of a cell. And, obviously, we need to add a CellDivision plugin that controls when and how a cell divides. Here, we specify that the cell should divide when CDK1 > 0.5 in the Condition of cell division.

One additional thing to specify is what happens when cell division occurs using the Triggers. Here, we specify that the target volume Vt of the two daughter cells is half the target volume of the mother cell (Vt/2), i.e. to model cleavage without cell growth.
Lastly, we add the CPM section, providing the temporal simulation. Cells shall preferably adhere to each other, such that we set at negative interaction energy for cells.
<CPM>
<Interaction>
<Contact type1="sbml_cell" type2="sbml_cell" value="-12.0"/>
</Interaction>
<ShapeSurface scaling="norm">
<Neighborhood>
<Order>6</Order>
</Neighborhood>
</ShapeSurface>
<MonteCarloSampler stepper="edgelist">
<MCSDuration value="0.1"/>
<MetropolisKinetics temperature="5"/>
<Neighborhood>
<Order>1</Order>
</Neighborhood>
</MonteCarloSampler>
</CPM>
This generates a simulation like this:
Check out CellCycle.xml to try yourself via:
- Morpheus Link or
- Morpheus GUI:
Examples→Multiscale→CellCycle.xmlor - Morpheus Model Repository.
Step 3: Intercellular Model (PDE)
The remaining two steps are:
- Allow cells to release a diffusive chemokine.
- Make this chemokine modulate the cell cycle.
Adding a Diffusive Field
First, let’s define a cytokine
In Morpheus, we define a Field g in the Global section and specify the diffusion coefficient Diffusion/rate as 100. The reaction step of is defined in the System where we provide a DiffEqn with the production and decay terms in the expression APC - 0.05*g:
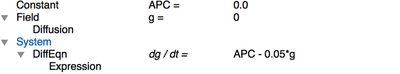
APC to be zero everywhere (Constant: APC=0.0), but this value is overwritten wherever there are cells (i.e. in the CellType scope).
This established the coupling between CPM and PDE: the movement and shape of CPM cells affect the production term in the PDE.
Modulating the Cell Cycle
The final step is to let the local concentration of the cytokine modulate the cell cycle.
We first need to compute the local cytokine concentration Mapper which allows us to reduce the spatial granularity by selecting the mapping statistics we want. Here, we specify the Mapper to take Field g as an input and assign the average value to the cell’s Property g_l – the local cytokine concentration.
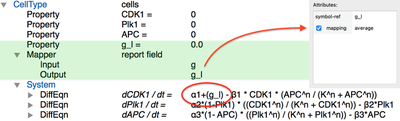
Finally, we let the local concentration of DiffEqn for CDK1 (see red outline). This implements the coupling between PDE and ODE: the extracellular cytokine concentration affects the intracellular cell cycle.
Here’s a video of a simulation of the full multiscale model we’ve constructed:
Check out CellCycle_PDE.xml to try yourself via:
- Morpheus Link or
- Morpheus GUI:
Examples→Multiscale→CellCycle_PDE.xml