Types of Boundary Conditions
‘Which types of boundary conditions does Morpheus provide?’
Morpheus provides three types of boundary conditions.
| Name | Synonym | Meaning |
|---|---|---|
| Periodic | Wrap-around | Lattice is wrapped around to opposite site, such that there is no border. |
| Constant | Dirichlet | Border states have specified constant values. |
| Noflux | Neumann | Derivative at border is zero. |
These can be specified in Space → Lattice → BoundaryConditions. These define the structure of the boundaries.
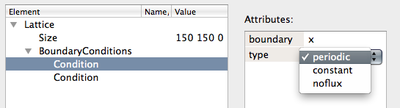
Space → Lattice → BoundaryConditions.
Note that there are six boundaries (x,-x, y, -y, z, -z,). All need to be specified, expect when periodic boundaries are used (in which case +x=-x, +y=-y, +z=-z).
Define Boundary Condition
To define boundaries, add entries in Space → Lattice → BoundaryConditions.
Define Boundary Values
To specify the values the boundaries should take, we distinguish between Fields (i.e. Reaction-Diffusion models) and cell-based models. Periodic boundaries do not use boundary values, since these are topologically connected.
Fields (Reaction-Diffusion Models, PDE)
When using constant boundary conditions, values used at the boundary of a reaction-diffusion model can be specified as expressions in Field → BoundaryValue. Assuming non-zero diffusion, this causes a flux across the boundary depending on the actual concentration gradient at that boundary.
The default value is 0.0.
When using noflux boundary conditions, the value plays no role in reactions-diffusion systems, since the flux is set to zero. However, the NeighborhoodReporter accesses these boundary values when computing mappings of the local neighborhood.
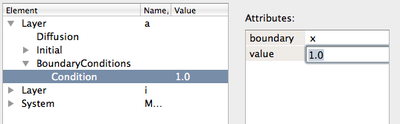
Field → BoundaryValue.
Cell-Based Models
Any medium cell type can be specified as noflux or constant boundary. First, define a cell type of type medium under CellTypes. To specify this at the boundary of a cell-based model with constant boundary conditions, use CellPopulatons → BoundaryValue.
Note that cells interact with the choosen boundary type, but only in the case of constant boundary the boundary cell type may extend / flow into the simulation space.