Predator-Prey Model by Rosenzweig

M. L. Rosenzweig (Author)

Open in Morpheus

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Introduction

This model implements an extension of the well-known Lotka-Volterra system.

It illustrates how to

create a simple ODE model and
log and plot data as time course.

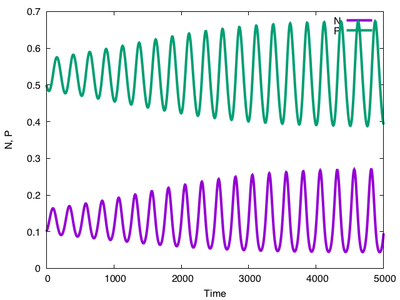
Description

The Rosenzweig model is the Lotka-Volterra model with logistic growth and type 2 functional response.

First, the Space and Time of a simulation is specified, here defined as a single lattice site and $5000 atu$ (arbitrary time units). In Global (see figure below), two Variables for predator and prey densities are set up. The differential equations themselves are specified in a System which consists of a number of Constants and two DiffEqn (differential equations) and are computed using the runge-kutta solver.

Output in terms of a text file as well as a plot is created by a Logger, the plugin in the Analysis section.

Things to try

Bring the system into a stable steady state (fixed point, no oscillations) by changing parameters in Global/System/Constant.

Reference

M. L. Rosenzweig: Paradox of Enrichment: Destabilization of Exploitation Ecosystems in Ecological Time. Science 171 (3969): 385-387, 1971.

Model

Get this model via:

Morpheus-Link or

Morpheus GUI: Examples → ODE → PredatorPrey.xml or

Download: PredatorPrey.xml

XML Preview

<MorpheusModel version="4">
    <Description>
        <Title>Example-PredatorPrey</Title>
        <Details>Example showing Predator-prey model by Rosenzweig.

The Rosenzweig model is the Lotka-Volterra model with logistic growth and type 2 functional response. 

Reference:
Rosenzweig, Michael. 1971. "The Paradox of Enrichment" Science Vol. 171: pp. 385–387


Illustrates how to 
- create a simple ODE model
- log and plot data as time course</Details>
    </Description>
    <Global>
        <Variable value="0.1" symbol="N"/>
        <Variable value="0.5" symbol="P"/>
        <System time-step="0.1" solver="Runge-Kutta [fixed, O(4)]">
            <Constant name="halftime" value="0.5" symbol="a"/>
            <Constant name="growth rate" value="0.1" symbol="r"/>
            <Constant name="consumption rate" value="0.1" symbol="c"/>
            <Constant name="conversion rate" value="0.05" symbol="b"/>
            <Constant name="mortality rate" value="0.01" symbol="m"/>
            <Constant name="Carrying capacity" value="0.8" symbol="K"/>
            <DiffEqn symbol-ref="N">
                <Expression>r*N*(1-N/K) - c*N / (a+N)*P
</Expression>
            </DiffEqn>
            <DiffEqn symbol-ref="P">
                <Expression>b*N / (a+N)*P - m*P</Expression>
            </DiffEqn>
            <!--    <Disabled>
        <Function symbol="c">
            <Expression>0.1 + time*0.00001</Expression>
        </Function>
    </Disabled>
-->
        </System>
        <Event trigger="when true" time-step="1">
            <Condition>N &lt; 0.001</Condition>
            <Rule symbol-ref="N">
                <Expression>0</Expression>
            </Rule>
        </Event>
    </Global>
    <Space>
        <Lattice class="linear">
            <Size value="1, 0, 0" symbol="size"/>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="5000" symbol="stoptime"/>
        <TimeSymbol symbol="time"/>
    </Time>
    <Analysis>
        <Logger time-step="5">
            <Input>
                <Symbol symbol-ref="N"/>
                <Symbol symbol-ref="P"/>
            </Input>
            <Output>
                <TextOutput file-format="csv"/>
            </Output>
            <Plots>
                <Plot time-step="-1">
                    <Style style="lines" line-width="2.0"/>
                    <Terminal terminal="png"/>
                    <X-axis>
                        <Symbol symbol-ref="time"/>
                    </X-axis>
                    <Y-axis>
                        <Symbol symbol-ref="N"/>
                        <Symbol symbol-ref="P"/>
                    </Y-axis>
                </Plot>
                <Plot time-step="-1">
                    <Style style="lines" line-width="2.0"/>
                    <Terminal terminal="png"/>
                    <X-axis>
                        <Symbol symbol-ref="N"/>
                    </X-axis>
                    <Y-axis>
                        <Symbol symbol-ref="P"/>
                    </Y-axis>
                    <Color-bar palette="rainbow">
                        <Symbol symbol-ref="time"/>
                    </Color-bar>
                </Plot>
            </Plots>
        </Logger>
        <ModelGraph include-tags="#untagged" format="svg" reduced="false"/>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Last updated on Mon, 13 May 2024