Tumor Growth: Unlimited Oxygen and Glucose Supply

N. Jagiella, D. Rickert, F. J. Theis, J. Hasenauer (Authors)

R. Müller, L. Brusch, E. Alamoudi, J. Hasenauer (Contributors)

DOI:10.1016/j.cels.2016.12.002

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Introduction

In Jagiella et al. 2017 a quantitative single cell-based mathematical model for multi-cellular tumor spheroids was parametrized by Bayesian inference for different scenarios of nutrition and oxygen supply. The simulations generate of the order of a million individual cells. Experimental data (growth kinetics, spatial patterns for cell proliferation, cell death, extracellular matrix density) were taken from a non-small cell lung cancer (NSCLC) cell line in earlier work Jagiella et al. 2016. The original open-source model is available on GitHub.

[Fig. 4a](https://www.cell.com/cell-systems/fulltext/S2405-4712(16)30412-4#fig4) shows the original model results (blue, and intermediate fitting states in grey) in comparison to the experimental data (green symbols, at day 17 for ECM and proliferation ratio pattern). ([CC BY-NC-ND 4.0](https://creativecommons.org/licenses/by-nc-nd/4.0/): [Jagiella et al. 2017](#reference)) — Fig. 4a shows the original model results (blue, and intermediate fitting states in grey) in comparison to the experimental data (green symbols, at day 17 for ECM and proliferation ratio pattern). (CC BY-NC-ND 4.0: Jagiella et al. 2017)

Description

Here, the Morpheus model quantitatively reproduces the published results for scenario I of unlimited oxygen and nutrient supply. Thus, the model focuses on cell mechanics, motility, proliferation and the secretion, turnover of extracellular matrix (ECM).

Jagiella et al. 2017 had modelled cell migration and spatial competition implicitly for point-like agents in a cellular automaton on a network, including long-range cell displacements to make room for cell divisions. In the Morpheus model, the Cellular Potts Model (CPM) formalism is used to represent moving and growing cells with spatial resolution and explicit, purely local competition for space. While most parameter values were maintained as published, to account for the different cell mechanics model, the proliferation rate k_div_max had to be re-adjusted. In addition, the observables ECM density and proliferation ratio as well as the initial radius of the spheroid R_init were rescaled by constant factors to match the experimental units.

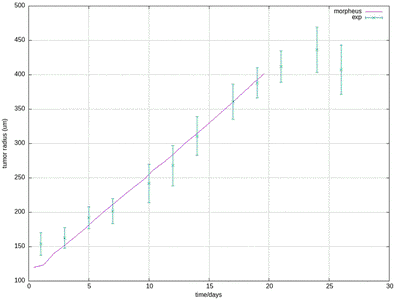
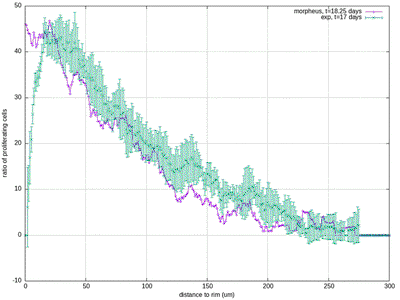
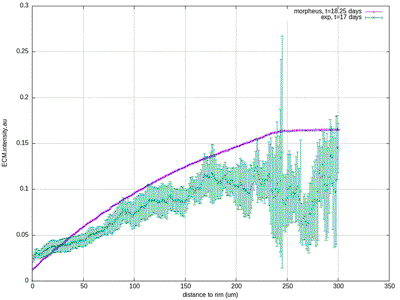
Below, the proliferation ratio histogram and comparative charts between simulation results and experimental data were created during simulation by the Morpheus plugin External. This plugin enables live data processing and visualization (beyong Morpheus' on-board capabilities) during the simulation by starting arbitrary external programs (here: awk scripts and gnuplot).

Units in the model are $[\text{space}] = \mathrm{\mu m}$, [time] = hours respectively days.
Parameter values were taken from Jagiella et al. 2017.
Boundary conditions are no-flux along the domain boundary by default. The model is here simulated in 2D and is ready for 3D.
Initial condition: a mix of proliferating and quiescent cells are placed in a circle with initial radius R_init at the center of the lattice.

Results

This movie of a Morpheus model simulation shows proliferating cells in red and quiescent cells in yellow, in the left panel. In the right panel, ECM density is color coded as indicated. Time in hours is given at the bottom.

The results for scenario I with abundant nutrients and oxygen from Jagiella et al. 2017 are quantitatively reproduced after rescaling of the observables. For illustration purposes we only show results from a single simulation run while the published plots show ensemble data of many runs.

Growth curve of tumor spheroid radius obtainied with the Morpheus model (line) vs. experimental data (symbols), matching the upper-left panel in Fig.4a above.

Proliferation ratio profile at day 17 obtained with the Morpheus model (line) vs. experimental data (symbols), matching the upper-middle panel in Fig.4a above.

ECM density profile at day 17 obtained with the Morpheus model vs. experimental data (symbols), matching the upper-right panel in Fig.4a above.

Note that the first day in this CPM dynamics is overshadowed (cf. radius curve) by the cell shape relaxation that is initialized simply with point-like cells. Alternative initializations with larger cells are of course possible.

Reference

This model reproduces a published result, originally obtained with a different simulator:

N. Jagiella, D. Rickert, F. J. Theis, J. Hasenauer: Parallelization and High-Performance Computing Enables Automated Statistical Inference of Multi-scale Models. Cell Systems 4 (2): 194-206.e9, 2017.

Model

Get this model via:

Morpheus-Link or

Download: tumor_spheroid_unlimited_supply.xml

XML Preview

<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
    <Description>
        <Title>Tumor Unlimited Supply</Title>
        <Details>Full title:        Tumor Growth: Unlimited Oxygen and Glucose Supply
Date: 	21.01.2022
Authors: 	N. Jagiella, D. Rickert, F. J. Theis, J. Hasenauer
Curators: 	R. Müller, L. Brusch, E. Alamoudi, J. Hasenauer
Software: 	Morpheus (open-source), download from https://morpheus.gitlab.io
ModelID: 	https://identifiers.org/morpheus/M0007
Reference:    This model reproduces the published results of scenario I, originally obtained with a different simulator:
                       N. Jagiella, D. Rickert, F. J. Theis, J. Hasenauer: Parallelization and High-Performance Computing Enables Automated Statistical Inference of Multi-scale Models. Cell Systems 4 (2): 194-206.e9, 2017.
https://doi.org/10.1016/j.cels.2016.12.002

The model is set up for 2D but in principle ready for 3D as well.
</Details>
    </Description>
    <Global>
        <Field symbol="e" name="ECM" value="0">
            <BoundaryValue boundary="x" value="0.0"/>
            <BoundaryValue boundary="-x" value="0.0"/>
            <BoundaryValue boundary="y" value="0.0"/>
            <BoundaryValue boundary="-y" value="0.0"/>
        </Field>
        <System time-step="1.0" solver="Euler [fixed, O(1)]">
            <DiffEqn symbol-ref="e">
                <Expression>ke_pro*c-ke_deg*e</Expression>
            </DiffEqn>
        </System>
        <Constant symbol="k_div_max" value="1.2e-2"/>
        <Constant symbol="k_re_max" value="1e-3"/>
        <Constant symbol="m_g" value="2"/>
        <Constant symbol="m_d" value="10"/>
        <Constant symbol="e_div" value="3.0e-3"/>
        <Constant symbol="L_div_num" value="L_div/length_unit"/>
        <Constant symbol="V_target" value="16"/>
        <Constant symbol="c" name="indicator of Prolif_cell or Quiesc_cell" value="0.0"/>
        <Constant symbol="c_nec" value="0.0"/>
        <Constant symbol="kg" value="1e-1"/>
        <Constant symbol="kmg" value="6.8e-2"/>
        <Constant symbol="L_init_num" value="L_init/length_unit"/>
        <Constant symbol="q_init" value="7.5e-1"/>
        <Constant symbol="ke_pro" value="5.0e-4"/>
        <Constant symbol="ke_deg" value="3.3e-3"/>
        <Variable symbol="V_spheroid" value="0"/>
        <Mapper name="V_spheroid">
            <Input value="cell.volume*(cell.type!=celltype.medium.id)"/>
            <Output symbol-ref="V_spheroid" mapping="sum"/>
        </Mapper>
        <Function symbol="radius.micrometer">
            <Expression>max(L_init_num_scaling_to_exp,sqrt(V_spheroid/pi))*length_unit</Expression>
        </Function>
        <Constant symbol="length_unit" value="16.8/sqrt(4*V_target/pi)"/>
        <Constant symbol="N_init" value="pi*L_init_num_scaling_to_exp^2/V_target"/>
        <Function symbol="time.day">
            <Expression>(time-t0)/24</Expression>
            <Annotation>To await the initial expansion of point-seeded cells, a transient of 20 time units is subtracted here and hidden via Analysis/Logger/Restriction.</Annotation>
        </Function>
        <Constant symbol="e_cell" value="0.0"/>
        <Variable symbol="meanprolif" value="0.0"/>
        <Constant symbol="prolif" value="0.0"/>
        <Constant symbol="t0" value="30"/>
        <Function symbol="e_cell_scaling_to_exp">
            <Expression>e_cell/0.7</Expression>
        </Function>
        <Function symbol="prolif_scaling_to_exp">
            <Expression>prolif*0.6</Expression>
        </Function>
        <Function symbol="L_init_num_scaling_to_exp">
            <Expression>L_init_num*10</Expression>
        </Function>
        <Constant symbol="N_prolif" value="N_init*(1 - q_init)"/>
        <Constant symbol="N_quiesc" value="N_init-N_prolif"/>
        <VectorMapper>
            <Input value="cell.center.x, cell.center.y, 0.0"/>
            <Output symbol-ref="com" mapping="average"/>
        </VectorMapper>
        <VariableVector symbol="com" value="0.0, 0.0, 0.0"/>
        <Function symbol="distance.to.rim.com.micrometer">
            <Expression>radius.micrometer-sqrt((cell.center.x-com.x)^2+(cell.center.y-com.y)^2)*length_unit</Expression>
        </Function>
        <Constant symbol="L_init" value="12"/>
        <Constant symbol="L_div" value="130"/>
    </Global>
    <Space>
        <Lattice class="square">
            <Size symbol="size" value="400, 400, 0"/>
            <BoundaryConditions>
                <Condition type="constant" boundary="x"/>
                <Condition type="constant" boundary="-x"/>
                <Condition type="constant" boundary="y"/>
                <Condition type="constant" boundary="-y"/>
            </BoundaryConditions>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime symbol="stoptime" value="500"/>
        <TimeSymbol symbol="time"/>
        <RandomSeed value="1234"/>
    </Time>
    <CellTypes>
        <CellType name="medium" class="medium">
            <Constant symbol="cell.volume" tags="new" value="0"/>
            <Property symbol="L" value="0.0"/>
            <Property symbol="medium_contact" tags="new" value="0.0"/>
            <Property symbol="m" value="0.0"/>
        </CellType>
        <CellType name="Quiesc_cell" class="biological">
            <VolumeConstraint target="V_target" strength="1" name="V_target"/>
            <ChangeCellType time-step="1.0" newCellType="Prolif_cell" name="-> Prolif_cell">
                <Triggers>
                    <Rule symbol-ref="prolif" name="p_re">
                        <Expression>rand_uni(0,1) &lt; (exp(-L/L_div_num)*(e_cell>e_div))</Expression>
                    </Rule>
                </Triggers>
                <Condition>rand_uni(0,1) &lt; k_re_max</Condition>
            </ChangeCellType>
            <Constant symbol="c" name="indicator for Global/Fields" value="1"/>
            <Property symbol="e_cell_inter" name="intermediate for ECM" value="0"/>
            <Mapper name="e_cell_inter">
                <Input value="e"/>
                <Output symbol-ref="e_cell_inter" mapping="average"/>
            </Mapper>
            <Property symbol="e_cell" value="0"/>
            <Event compute-time="on-execution" trigger="when-true" time-step="1" name="e_cell">
                <Condition>1</Condition>
                <Rule symbol-ref="e_cell">
                    <Expression>e_cell_inter</Expression>
                </Rule>
            </Event>
            <Property symbol="m" value="1"/>
            <Property symbol="prolif" value="-1"/>
            <Property symbol="medium_contact" tags="new" value="0.0"/>
            <NeighborhoodReporter name="medium_contact" tags="new">
                <Input noflux-cell-medium="false" scaling="cell" value="cell.type == celltype.medium.id"/>
                <Output symbol-ref="medium_contact" mapping="maximum"/>
            </NeighborhoodReporter>
            <Property symbol="L" value="0.0"/>
            <NeighborhoodReporter time-step="1.0" name="propagate distance">
                <Input scaling="cell" value="L"/>
                <Output symbol-ref="LTmp" mapping="minimum"/>
            </NeighborhoodReporter>
            <Property symbol="LTmp" value="1000000"/>
            <System time-step="1.0" solver="Dormand-Prince [adaptive, O(5)]">
                <Rule symbol-ref="L">
                    <Expression>if(medium_contact==1,sqrt(cell.volume/pi),LTmp+1.28*sqrt(4*cell.volume/pi))</Expression>
                </Rule>
            </System>
            <Function symbol="distance.to.rim.hop.micrometer">
                <Expression>L*length_unit</Expression>
            </Function>
        </CellType>
        <CellType name="Prolif_cell" class="biological">
            <Property symbol="e_cell_inter" name="intermediate for ECM" value="0"/>
            <Mapper name="e_cell_inter">
                <Input value="e"/>
                <Output symbol-ref="e_cell_inter" mapping="average"/>
            </Mapper>
            <Property symbol="e_cell" value="0"/>
            <Event compute-time="on-execution" trigger="when-true" time-step="1" name="e_cell">
                <Condition>1</Condition>
                <Rule symbol-ref="e_cell">
                    <Expression>e_cell_inter</Expression>
                </Rule>
            </Event>
            <Property symbol="m" value="1"/>
            <Property symbol="prolif" value="1"/>
            <VolumeConstraint target="V_target*(1+m>=m_g)" strength="1" name="V_target*(1+m>=m_g)"/>
            <CellDivision name="m == m_d" division-plane="random">
                <Condition>m == m_d*(e_cell>-1)</Condition>
                <Triggers>
                    <Rule symbol-ref="m">
                        <Expression>1</Expression>
                    </Rule>
                    <!--    <Disabled>
        <Rule symbol-ref="prolif">
            <Expression>rand_uni(0,1) &lt; (exp(-L/L_div_num)*(e_cell>e_div)*(ka>ka_div)*(l_cell&lt;l_div)*(nwo_max>nwo))</Expression>
        </Rule>
    </Disabled>
-->
                    <Rule symbol-ref="prolif">
                        <Expression>rand_uni(0,1) &lt; (exp(-L/L_div_num)*(e_cell>e_div))</Expression>
                    </Rule>
                </Triggers>
            </CellDivision>
            <ChangeCellType time-step="1.0" newCellType="Quiesc_cell" name="-> Quiesc_cell">
                <Condition>prolif == 0</Condition>
                <Triggers>
                    <Rule symbol-ref="m">
                        <Expression>1</Expression>
                    </Rule>
                </Triggers>
            </ChangeCellType>
            <Constant symbol="c" name="indicator for Global/Fields" value="1"/>
            <Event compute-time="on-execution" trigger="when-true" time-step="1" name="m -> m+1">
                <Condition>1</Condition>
                <Rule symbol-ref="m">
                    <Expression>m+(rand_uni(0,1)&lt;k_div_max*1*m_d)</Expression>
                </Rule>
            </Event>
            <Property symbol="medium_contact" tags="new" value="0.0"/>
            <NeighborhoodReporter name="medium_contact" tags="new">
                <Input noflux-cell-medium="false" scaling="cell" value="cell.type == celltype.medium.id"/>
                <Output symbol-ref="medium_contact" mapping="maximum"/>
            </NeighborhoodReporter>
            <NeighborhoodReporter time-step="1.0" name="L-Neighbours">
                <Input scaling="cell" value="L"/>
                <Output symbol-ref="LTmp" mapping="minimum"/>
            </NeighborhoodReporter>
            <Property symbol="LTmp" name="temp for propagating distance" value="1000000"/>
            <System time-step="1.0" solver="Dormand-Prince [adaptive, O(5)]">
                <Rule symbol-ref="L">
                    <Expression>if(medium_contact==1,sqrt(cell.volume/pi),LTmp+1.28*sqrt(4*cell.volume/pi))</Expression>
                </Rule>
            </System>
            <Property symbol="L" value="0.0"/>
            <Function symbol="distance.to.rim.hop.micrometer">
                <Expression>L*length_unit</Expression>
            </Function>
            <Property symbol="" value="0.0"/>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0">
            <Contact type2="Prolif_cell" type1="Prolif_cell" value="10"/>
            <Contact type2="Quiesc_cell" type1="Prolif_cell" value="10"/>
            <Contact type2="Quiesc_cell" type1="Quiesc_cell" value="10"/>
            <Contact type2="medium" type1="Prolif_cell" value="6"/>
            <Contact type2="medium" type1="Quiesc_cell" value="6"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="0.2"/>
            <Neighborhood>
                <Order>1</Order>
            </Neighborhood>
            <MetropolisKinetics temperature="3"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population type="Prolif_cell" size="1">
            <!--    <Disabled>
        <InitProperty symbol-ref="prolif">
            <Expression>1 - (rand_uni(0,1) &lt; q_init)</Expression>
        </InitProperty>
    </Disabled>
-->
            <InitCircle mode="random" number-of-cells="N_prolif">
                <Dimensions center="size.x/2,size.y/2,0" radius="L_init_num_scaling_to_exp"/>
            </InitCircle>
        </Population>
        <Population type="Prolif_cell" size="1">
            <!--    <Disabled>
        <InitProperty symbol-ref="prolif">
            <Expression>1 - (rand_uni(0,1) &lt; q_init)</Expression>
        </InitProperty>
    </Disabled>
-->
            <InitCircle mode="random" number-of-cells="N_quiesc">
                <Dimensions center="size.x/2,size.y/2,0" radius="L_init_num_scaling_to_exp"/>
            </InitCircle>
        </Population>
    </CellPopulations>
    <Analysis>
        <ModelGraph include-tags="#untagged,new" reduced="false" format="png"/>
        <Logger time-step="20">
            <Input>
                <Symbol symbol-ref="time.day"/>
                <Symbol symbol-ref="radius.micrometer"/>
            </Input>
            <Output>
                <TextOutput/>
            </Output>
            <Restriction condition="time>(t0-1)"/>
        </Logger>
        <Logger time-step="438">
            <Input>
                <Symbol symbol-ref="e_cell_scaling_to_exp"/>
                <Symbol symbol-ref="distance.to.rim.com.micrometer"/>
                <Symbol symbol-ref="distance.to.rim.hop.micrometer"/>
            </Input>
            <Output>
                <TextOutput/>
            </Output>
            <Restriction condition="time>(t0-1)"/>
        </Logger>
        <Logger time-step="438">
            <Input>
                <Symbol symbol-ref="prolif_scaling_to_exp"/>
                <Symbol symbol-ref="distance.to.rim.com.micrometer"/>
                <Symbol symbol-ref="distance.to.rim.hop.micrometer"/>
            </Input>
            <Output>
                <TextOutput file-separation="time" file-numbering="time"/>
            </Output>
            <Restriction condition="time>(t0-1)"/>
        </Logger>
        <External time-step="438">
            <Command>export LANG=C; awk -f ./prolif.awk 10 300 1 %time ; 
		     awk -f ./ecm.awk 10 300 1 %time </Command>
            <Environment variable="DISPLAY" value="empty"/>
        </External>
        <External time-step="438">
            <Command>export LANG=C; awk -f ./cmp.awk 438</Command>
        </External>
        <!--    <Disabled>
        <Gnuplotter time-step="100">
            <Plot>
                <Cells value="e_cell_scaling_to_exp"/>
            </Plot>
            <Terminal name="png"/>
            <Plot>
                <Cells value="cell.type"/>
            </Plot>
        </Gnuplotter>
    </Disabled>
-->
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

2D 3D ABC SMC Algorithm Approximate Bayesian Computation Approximate Bayesian Computation Sequential Monte Carlo Algorithm Bayesian Parameter Estimation Benchmark Cell Culture Growth Curve High Performance Computing Histological Data HPC Hybrid Deterministic-Stochastic Behavior Mechanistic Model Media Droplets Medium Model-Based Data Integration Monte Carlo Monte Carlo Algorithm Multi-Scale Model Nutrient Environment pABC SMC Algorithm Parallel Approximate Bayesian Computation Sequential Monte Carlo Algorithm Parallelization Parameter Estimation Published Models Statistical Inference Tumor Tumor Spheroid Tumor Spheroid Growth

Last updated on Mon, 13 May 2024