Coupling Spatial Models: Autocrine Chemotaxis

Persistent Identifier

Use this permanent link to cite or share this Morpheus model:

Introduction

This example models a cellular Potts model for autocrine chemotaxis by coupling a CPM to a diffusive chemoattractant.

Cell cluster due to chemotaxis towards self-produced chemoattractant.

Description

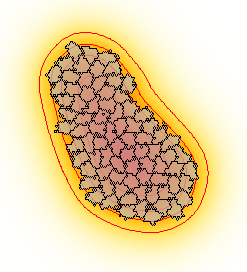
It exemplifies the combination of a CPM with a PDE through the chemotaxis towards a diffusive chemoattractant produced by cells. The CellType has a Property $p$ (production rate) which is positive within biological cells, and is zero in the medium cell type. The symbol $p$ can than be used in the PDE as the production term for species or Layer $U$. In this way, $U$ is produced in each lattice node that is occupied by a cell, and is not produced outside of cells. At the same time, cells perform Chemotaxis towards the chemoattractant $U$.

The simulation is visualized using some advanced Gnuplotter feature. Cells are superimposed on the PDE and appear as transparent domains (see opacity). Moreover, the concentration gradient of the PDE is emphasized by the use of isolines that draws contours as positions with equal concentration.

Model

Get this model via:

Morpheus-Link or

Morpheus GUI: Examples → Multiscale → AutocrineChemotaxis.xml or

Download: AutocrineChemotaxis.xml

XML Preview

<MorpheusModel version="3">
    <Description>
        <Title>Example-AutocrineChemotaxis</Title>
        <Details></Details>
    </Description>
    <Global>
        <Field symbol="U" value="0" name="chemoattractant">
            <Diffusion rate="0.1"/>
        </Field>
        <System solver="euler" time-step="10.0">
            <DiffEqn symbol-ref="U">
                <Expression>p - d*U</Expression>
            </DiffEqn>
            <Constant symbol="d" value="0.01" name="degradation U"/>
        </System>
        <Constant symbol="cell_density" value="0.003"/>
    </Global>
    <Space>
        <Lattice class="square">
            <Size symbol="size" value="200 200 0"/>
            <BoundaryConditions>
                <Condition boundary="x" type="periodic"/>
                <Condition boundary="y" type="periodic"/>
            </BoundaryConditions>
            <NodeLength value="1.0"/>
            <Neighborhood>
                <Distance>2.5</Distance>
            </Neighborhood>
        </Lattice>
        <SpaceSymbol symbol="space"/>
    </Space>
    <Time>
        <StartTime value="0"/>
        <StopTime value="2.5e4"/>
        <SaveInterval value="0"/>
        <RandomSeed value="0"/>
        <TimeSymbol symbol="time"/>
    </Time>
    <CellTypes>
        <CellType class="biological" name="cells">
            <!--    <Disabled>
        <Property symbol="cell" value="1.0"/>
    </Disabled>
-->
            <Property symbol="c" value="100.0" name="chemotactic strength"/>
            <Property symbol="p" value="0.01" name="production chemoattractant"/>
            <Property symbol="neighbors" value="0" name="number of neighboring cells"/>
            <VolumeConstraint target="60" strength="1"/>
            <SurfaceConstraint target="0.85" mode="aspherity" strength="1"/>
            <Chemotaxis field="U" contact-inhibition="false" strength="c" retraction="true"/>
            <NeighborhoodReporter>
                <Input scaling="cell" value="cell.type == celltype.cells.id"/>
                <Output symbol-ref="neighbors" mapping="sum"/>
            </NeighborhoodReporter>
        </CellType>
        <CellType class="medium" name="medium">
            <Constant symbol="neighbors" value="0.0"/>
            <Constant symbol="p" value="0.0" name="production"/>
        </CellType>
    </CellTypes>
    <CPM>
        <Interaction default="0.0">
            <Contact type1="cells" type2="medium" value="-10"/>
            <Contact type1="cells" type2="cells" value="-20"/>
        </Interaction>
        <MonteCarloSampler stepper="edgelist">
            <MCSDuration value="1.0"/>
            <Neighborhood>
                <Order>2</Order>
            </Neighborhood>
            <MetropolisKinetics temperature="10.0"/>
        </MonteCarloSampler>
        <ShapeSurface scaling="norm">
            <Neighborhood>
                <Distance>2.5</Distance>
            </Neighborhood>
        </ShapeSurface>
    </CPM>
    <CellPopulations>
        <Population size="0" type="cells">
            <InitRectangle mode="regular" number-of-cells="cell_density * size.x * size.y">
                <Dimensions size="size.x, size.y, 0" origin="0.0, 0.0, 0.0"/>
            </InitRectangle>
        </Population>
    </CellPopulations>
    <Analysis>
        <Gnuplotter time-step="500" decorate="false">
            <Terminal opacity="0.55" persist="true" name="png"/>
            <Plot>
                <Field symbol-ref="U" isolines="5" min="0.0" surface="true"/>
                <Cells>
                    <ColorMap>
                        <Color value="2.0" color="gray"/>
                        <Color value="0" color="gray"/>
                    </ColorMap>
                </Cells>
            </Plot>
        </Gnuplotter>
        <DependencyGraph format="svg" exclude-plugins="Gnuplotter"/>
    </Analysis>
</MorpheusModel>

Downloads

Files associated with this model:

Built-In Examples Multiscale Models

Last updated on Mon, 13 May 2024