Integrate and Fire
Persistent Identifier
Use this permanent link to cite or share this Morpheus model:
Simple model for neuronal firing
Introduction
This is one of the simplest models used to depict neuronal firing.
Description
A simple model for neuronal firing consists of the basic ‘integrate-and-fire’ system ODE:
$$\begin{align} \frac{dV}{dt}=a_1, V=0 \text{ whenever } V \geq V_t \end{align}$$
Results
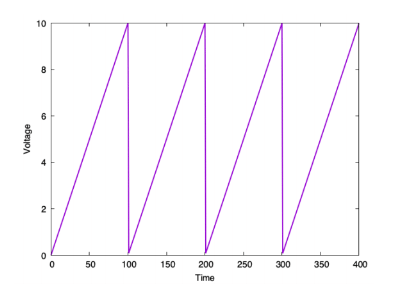
Here, the voltage builds up at a constant rate $a_1$. Once the voltage $V$ reaches a set value (in this example, $V_t = 10$), it is reset to zero, as shown in the following figure.
Model
IntegrateAndFire.xml
XML Preview
<?xml version='1.0' encoding='UTF-8'?>
<MorpheusModel version="4">
<Description>
<Title>Integrate and fire</Title>
<Details>Full title: Integrate and Fire
Authors: L. Edelstein-Keshet
Contributors: Y. Xiao
Date: 11.05.2022
Software: Morpheus (open-source). Download from https://morpheus.gitlab.io
Model ID: https://identifiers.org/morpheus/M2004
Reference: L. Edelstein-Keshet: Mathematical Models in Cell Biology
Comment: Basic integrate and fire model. This is one of the simplest models used to depict neuronal firing. Voltage, V, is constantly increasing until it gets to some threshold, Vt. Then it is reset to zero. Simulation shows how to reset a variable that satisfies a differential equation so as to produce a discontinuous output.</Details>
</Description>
<Global>
<Variable symbol="Voltage" name="Voltage" value="0"/>
<Variable symbol="Vt" name="Voltage at reset" value="10"/>
<System time-step="4e-2" time-scaling="1" solver="Runge-Kutta [fixed, O(4)]">
<Constant symbol="a1" value="0.1"/>
<Annotation>
Specify the differential equation for the variable. In this case,
Voltage is just increasing at a constant rate a1.
</Annotation>
<DiffEqn symbol-ref="Voltage">
<Expression>a1</Expression>
</DiffEqn>
</System>
<Event trigger="when-true" name="reset Voltage">
<Condition history="false">Voltage>Vt</Condition>
<Rule symbol-ref="Voltage">
<Expression>0</Expression>
</Rule>
</Event>
</Global>
<Time>
<StartTime value="0"/>
<StopTime symbol="stoptime" value="400"/>
<TimeSymbol symbol="time"/>
</Time>
<Analysis>
<Logger time-step="1">
<Input>
<Symbol symbol-ref="Vt"/>
</Input>
<Plots>
<Plot time-step="-1">
<Style line-width="2.0" style="lines"/>
<Terminal terminal="png"/>
<X-axis>
<Symbol symbol-ref="time"/>
</X-axis>
<Y-axis>
<Symbol symbol-ref="Voltage"/>
</Y-axis>
</Plot>
</Plots>
<Output>
<TextOutput/>
</Output>
</Logger>
<ModelGraph format="dot" reduced="false" include-tags="#untagged"/>
</Analysis>
<Space>
<Lattice class="linear">
<Neighborhood>
<Order>1</Order>
</Neighborhood>
<Size symbol="size" value="100, 0.0, 0.0"/>
</Lattice>
<SpaceSymbol symbol="space"/>
</Space>
</MorpheusModel>

Downloads
Files associated with this model: